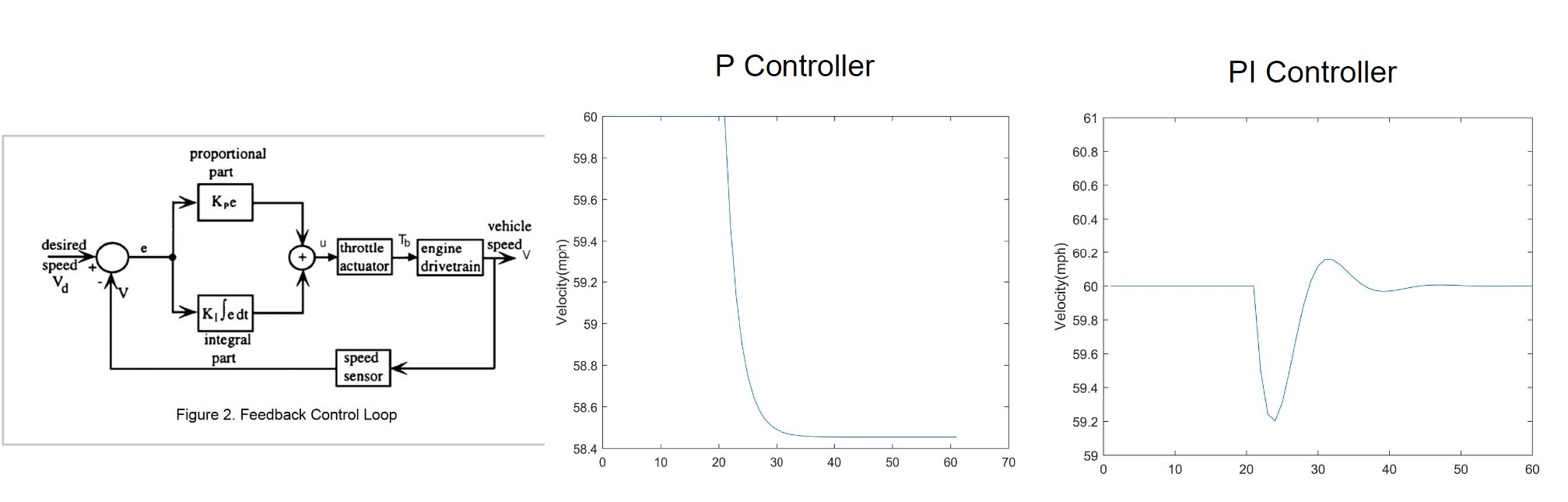
- Designed a PI controller in MATLAB & Simulink to achieve efficient tracking, quick response, stability, and disturbance rejection for varying road profiles
- But what if we need to include constraints and we don’t really need to linearize the system
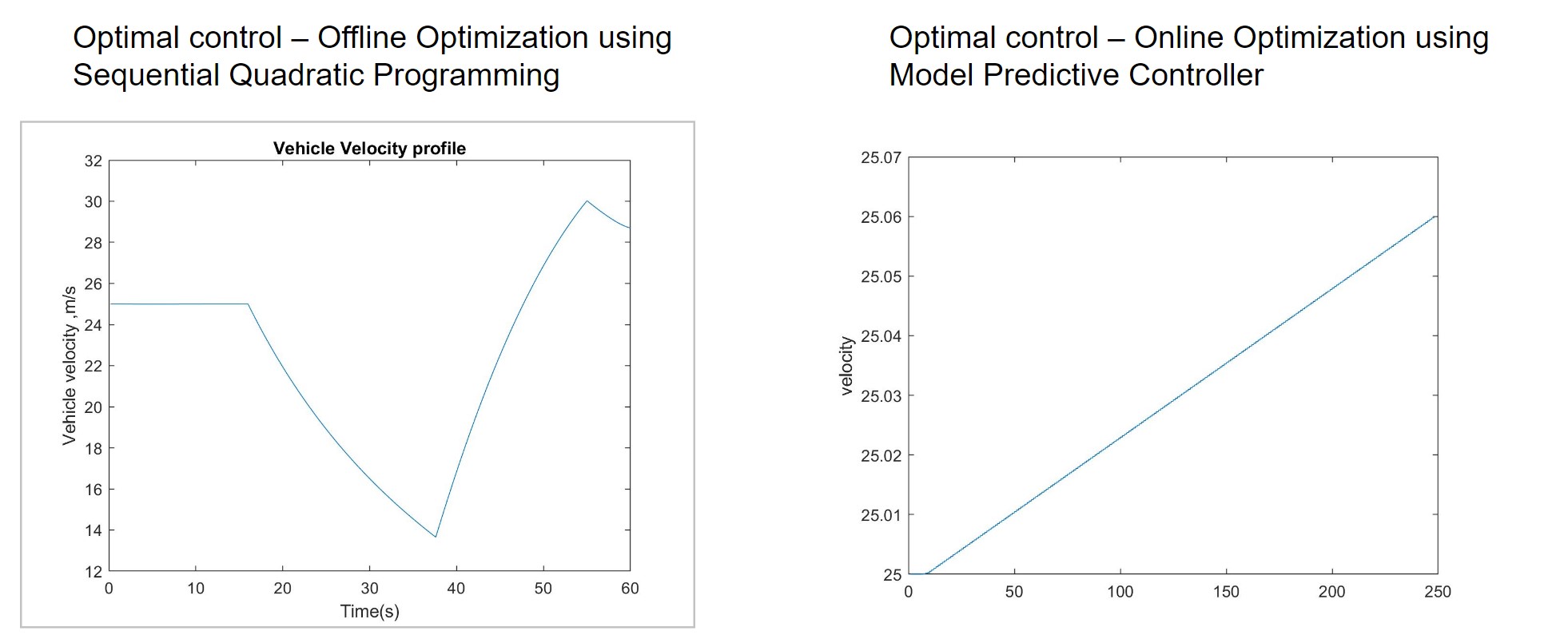
- Implemented Optimal control using SQP but can’t handle the disturbance
- Incorporated Model predictive Controller to achieve optimal velocity tracking the use of control and state constraints -speed limit of 20 – 30 m/s
- Implemented MPC using the Level-2 s-function in MATLAB
- Feedback loop setup using Triggered subsystem in Simulink
- A triggered subsystem is something that gets triggered at every time step.
- To tackle using fmincon inside Simulink, used the Level 2s function
- It has the level 2 s function that creates a wrapper for functions in MATLAB for its use inside Simulink
- Thus fmincon which basically does SQP is done at every time step for MPC here
- But since we have feedback, it is able to achieve disturbance rejection and also has a way to include constraints since it uses SQP
MPC parameters selection
- Time step size
- Rise time /20<= Step size <= Rise time /10 – Based on open-loop response
- Prediction horizon – How far the controller predicts into the future
- 20 to 30 samples covering the open loop transient system response
- Control horizon
- Number of control steps executed
- Only the first few control inputs have a significant impact
- So keeping it low will help avoid extra computation
- Usually, keep it to 10 to 20 % of the prediction horizon
- Constraints – Hard and soft constraints
- All hard constraints might lead to an infeasible solution for the optimization problem
- Soft constraints on outputs
- Avoid using hard constraints on both inputs and the rate of change of inputs
- Weighting parameters